Թեմա՝ Երկու կետերի միջեւ եղած հեռավորությունը։

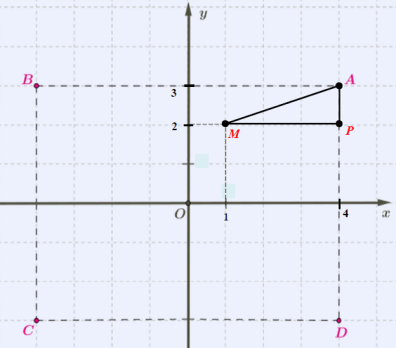
Հաշվենք MA հեռավորությունը M(1;2) և A(4;3) կետերի միջև:

Այդ կետերից տանենք կոորդինատային առանցքներին զուգահեռ հատվածներ և դիտարկենք առաջացած APM ուղղանկյուն եռանկյունը:

Հաշվենք APM եռանկյան MP և AP էջերը՝ MP=4−1=3, AP=3−2=1

Ունենալով APM ուղղանկյուն եռանկյան էջերը, Պյութագորասի թեորեմի միջոցով, գտնում ենք եռանկյան MA ներքնաձիգը՝

MA=√MP²+AP²=√3²+1²=√10

Այս օրինաչափությունը տեղի ունի նաև ընդհանուր դեպքում:

Եթե կոորդինատային հարթության վրա տրված են երկու կետեր՝ K(x0;y0) և L(x1;y1), ապա այդ կետերի միջև dKL հեռավորությունը կարելի է հաշվել հետևյալ բանաձևով՝

d_KL=√(x₁−x₀)²+(y₁−y₀)²

Այսպիսով, հարթության վրա տրված երկու կետերը միացնող հատվածի երկարությունը հավասար է՝ d_KL=√(x₁−x₀)²+(y₁−y₀)²

Առաջադրանքներ

1․ Գտնել կոորդինատային հարթության վրա M(5;12) կետի հեռավորությունը կոորդինատների սկզբնակետից:

2․ Հաշվիր հեռավորությունները հետևյալ կետերի միջև:

ա) A(8;1) և B(5;5);  բ) M(5;5) և N(1;8)

3․ Գտնել կոորդինատային հարթության վրա A(21;23) և B(24;27) ծայրակետերով հատվածի երկարությունը:

4․ Գտնել MNP եռանկյան պարագիծը, եթե M (7;5), N(4,1), P(10,9)։

5․ Գտնել x-ը, եթե A(2,1) և B(x;1) կետերի հեռավորությունը 2 է։